Exercises 15 18 Evaluate the Integral Using the Method Described
The improper integral converges if this limit is a finite real number. 4Use the residue theorem to compute Z C gzdz.
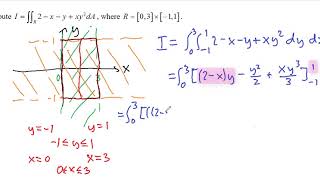
Double Integrals Volume And Average Value
3The contour will be made up of pieces.
. D v 2 3 e 3 x d x. We can evaluate this new integral by using integration by parts again. In the preceding section we used definite integrals to find the area between two curves.
In Exercises 13 18 a region of the Cartesian plane is described. X sec θ. Use Gauss quadrature method to solve examples of approximate integrals.
A A 625 b 42 meters c 12037 kilometers per hour. Using the result of Example 1 you have. Why would we want to integrate a function.
B Single application of the trapezoidal rule. 152 Double Integrals over General Regions 895 In Exercises 67 and 68 sketch the region of integration and the solid whose volume is given by the double integral. View HW4solutionpdf from GENERAL EN 235 at Qatar University.
532 Evaluate a double integral in polar coordinates by using an iterated integral. Find the volume of a solid of revolution with a cavity using the washer method. The integral is the area of the triangle 19.
For some of them it may be necessary to break the integral up into two parts. Evaluate the integral d x x x 2 1 d x x x 2 1 using the substitution x sec θ. 533 Recognize the format of a double integral over a general polar region.
Derive the Gauss quadrature method for integration and be able to use it to solve problems and 2. X2 sin xdx solution Let u x2 and v sin x. Fundamental Theorem of Calculus Part 1.
In the limit the definite integral equals area A1 A 1 minus area A2 A 2 or the net signed area. We must apply Integration by Parts again to evaluate. Fxx3 3x2 2x6 16.
Exercise 192 35 Evaluate the following integral. Use the method described in Notes I to supply the limits of integration. ASlice the solid parallel to the triangular faces.
It should be such that we can computeZ gzdzover each of the pieces except the part on the real axis. 415 parts per million 19. Example 2 The Integral of an Integral.
V 2 3 e 3 x d x 2 9 e 3 x. Y dy dx 2 2y2 sin xy dy dx x 41-2 xe2y dy dx 0 49. Otherwise the improper integral diverges.
Then 2 0 f xdx lim n n Σ i1f ciΔx A1 A2 0 2 f x d x lim n Σ n i 1 f c i Δ x A 1 A 2. 18The gure below shows a solid with both rectangular and triangular cross sections. Next evaluate the same integral using the substitution x csc θ.
The integral in Example 2 is an iterated integral. In Exercises 4756 sketch the region of integration reverse the order of integration and evaluate the integral. Using different substitutions Show that the integral Lx2 - 1x 1-23 dx can be evaluated with any of the following substitutions.
To do this choose u x u x and d v 2 3 e 3 x d x. The quantity A1 A2 A 1 A 2 is called the net signed area. Finding volume of a solid of revolution using a disc method.
5Combine the previous steps to deduce the value of the integral we want. U cosh-1 x What is the value of the integral. Use the shell method to write and evaluate the definite integral that represents the volume of the solid generated by revolving the plane region about the x -axis.
Sketch one slice and calculate its volume in terms of x the distance of the slice from one end. 534 Use double integrals in polar coordinates to calculate areas and volumes. Evaluate the integral exactly.
U 1x 1 b. In Exercises 1318 write a Riemann sum and then a definite integral representing the volume of the region using the slice shown. A R is the triangle with vertices at the origin 02 and.
An improper integral is defined in terms of a limit. U x - 1x 1k for k 1 12 13 -13 -23 and -1 c. Use the Shell Method to find the volume of the solid of revolution formed by rotating the region about each of the given axes.
Finding volume of a solid of revolution using a shell method. 3A-1 Evaluate each of the following iterated integrals. 4 This application of the method of slicing is called the washer method.
Considering xto be constant and integrating with respect to. As mentioned earlier the Fundamental Theorem of Calculus is an extremely powerful theorem that establishes the relationship between differentiation and integration and gives us a way to evaluate definite integrals without using Riemann sums or calculating areas. In each case begin by sketching the region.
2Pick a closed contour Cthat includes the part of the real axis in the integral. The volume can be computed as. U tan-1 x d.
U tan-1 x - 12 f. 6x2 2y dy dx b lnI2 Ln sin t t cos U dt du 3A-2 Express each double integral over the given region R as an iterated integral using the given order of integration. Then write and evaluate an integral giving the volume of the solid.
Determine the volume of a solid by integrating a cross-section the slicing method. We must evaluate two integrals as we have two different sample slices. Use the method described in Notes I to supply the limits of integration.
If a region in the plane is revolved about a given line the resulting solid is a solid of revolution and the line is called the axis of revolution. Then we have u x2 v cosx u 2xv sin x Using Integration by Parts we get x2 sin xdx x2cosx 2xcosxdxx2 cosx 2 xcosxdx. Thus d u d x d u d x and v 2 3 e 3 x d x 2 9 e 3 x.
Integration is the process of measuring the area under a function plotted on a graph. Up to 24 cash back Using Integration by Parts we get xsin3 xdx xcos3 x 1cos3 xdx xcos3 xsin3 xC 13. Fx1 3 x3 5 2 x2 4x.
BRepeat part a for horizontal slices. Example 1 Integrating with Respect to y. The integral is the area of the triangle 9.
Use the solving method described in. Regions are parts of cones cylinders spheres and pyramids 10 m Question. U cos-1 x g.
In the following exercises evaluate the integral using area formulas. An integral over an infinite interval or an integral of a function containing an infinite discontinuity on the interval. U tan-1 2x e.
72 Finding Volume using the Washer Method Example 1 Find the volume of the solid formed by revolving the region bounded by the graphs y x and y x2 about the x-axis. Finding volume of a solid of revolution using a washer method. Find the volume of a solid of revolution using the disk method.
Improper Integrals Calculus Volume 2
Double Integrals Over General Regions Calculus Volume 3

Example 38 Evaluate Integral X4 X 1 4 X5 Dx Examples

5 2 The Definite Integral Calculus Volume 1
Improper Integrals Calculus Volume 2

Rd Sharma Solutions For Class 10 Chapter 7 Statistics Exercise 7 5 Pdf Download

Ex 7 11 18 Class 12 Evaluate Definite Integral X 1 From 0 To 4
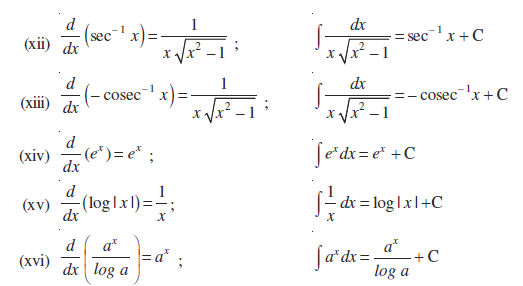
Integrals Ncert Class 12 Maths

Definite Integral Of Piecewise Function Video Khan Academy
5 2 The Definite Integral Calculus Volume 1

Average Value And Area Revisited
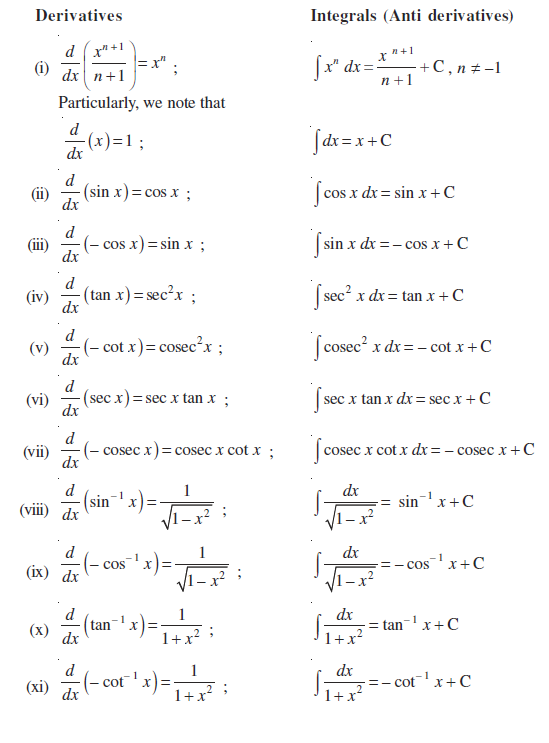
Integrals Ncert Class 12 Maths

Ex 7 11 18 Class 12 Evaluate Definite Integral X 1 From 0 To 4
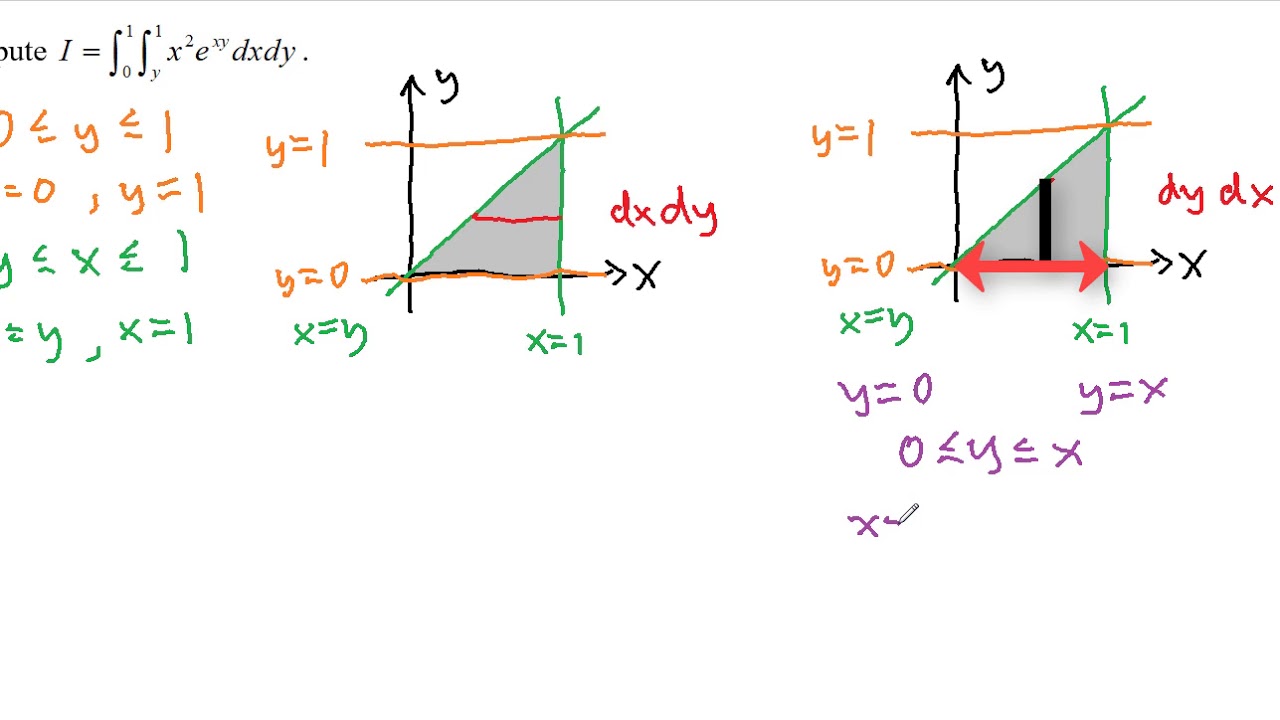
Double Integrals Volume And Average Value
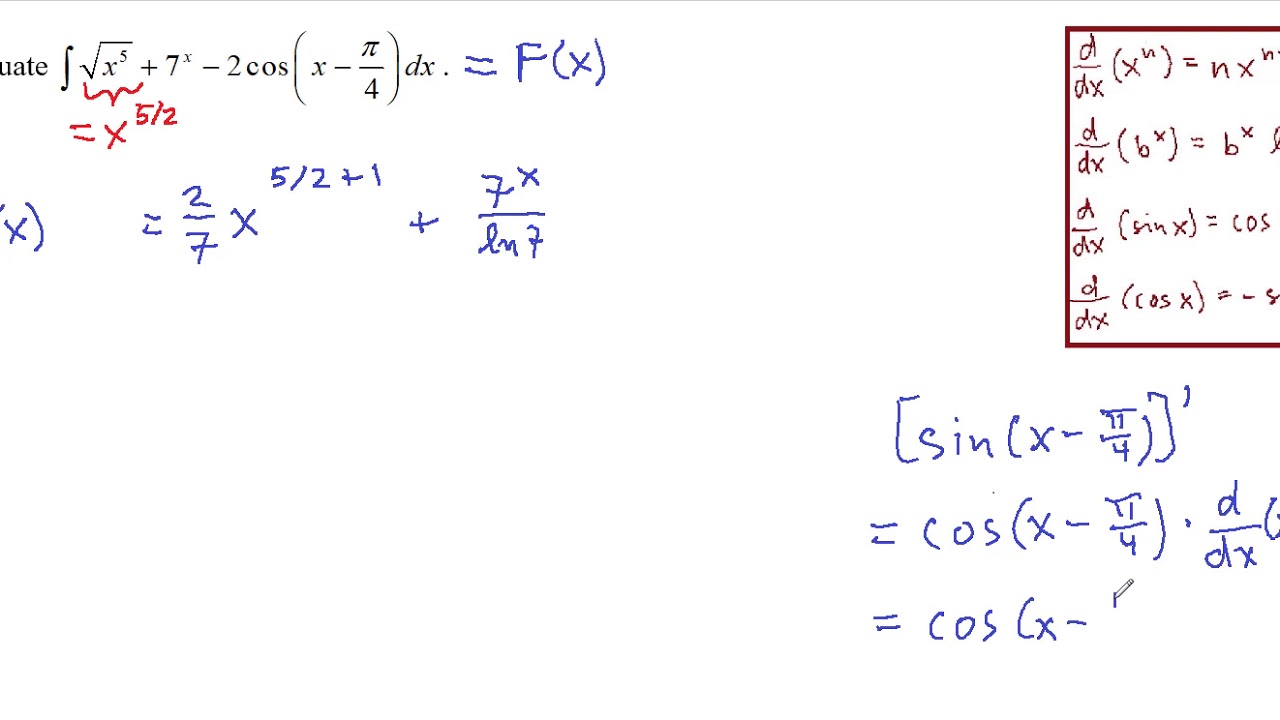
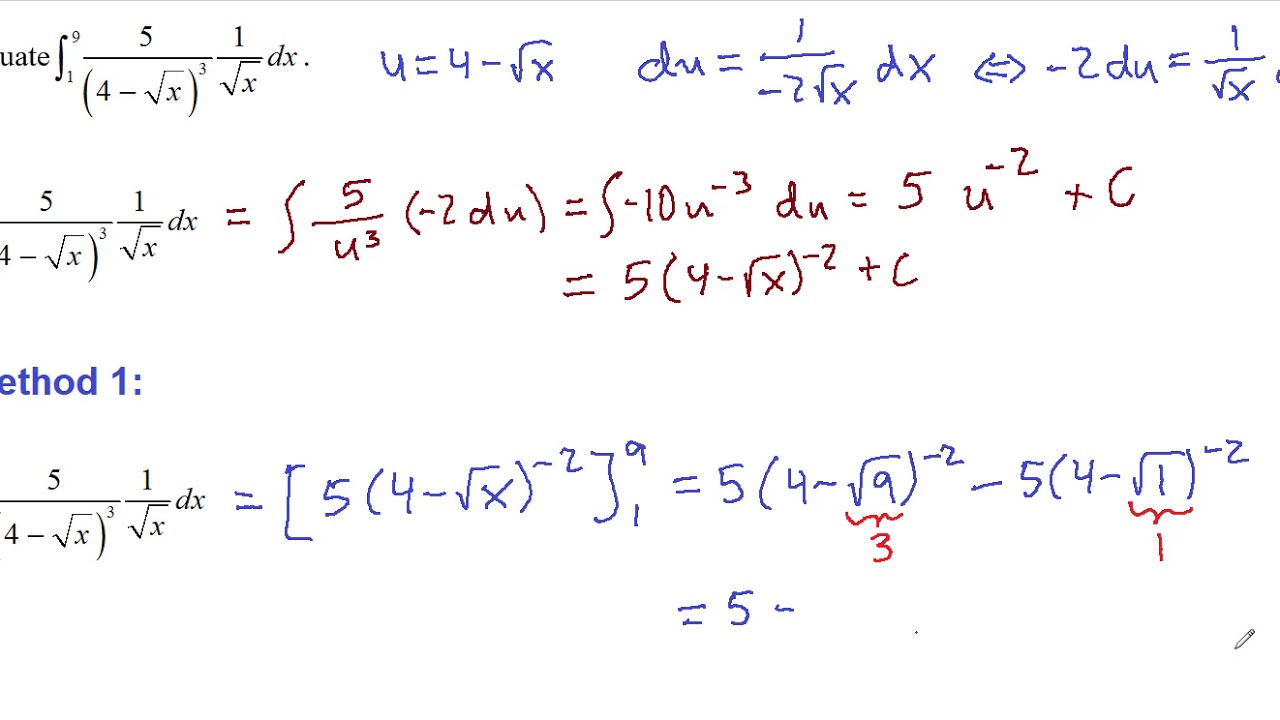
Comments
Post a Comment